Welcome

Welcome to the homepage of Owen Lewis. I am an applied mathematician and currently an Assistant Professor in the Department of Mathematics & Statistics at the University of New Mexico. My research interests lie at the intersection of mathematics, biology, and physics. Please see my research page for more details.

I am also an educator who feels strongly that mathematics and mathematical thinking are integral components of STEM education. My teaching page contains details regarding the various courses that I have taught in a classroom setting.

My outreach page contains details of the various mentorship and outreach programs that I take part in to expose a wider audience to mathematics.

Please feel free to look around.

My Research

My research interests involve using the techniques of mathematics to explore how the laws of physics inform biological function. As a general rule, this means that I design mathematical models to describe biological systems of interest, then develop the mathematical tools necessary to solve, analyze, or simulate said models. Finally, these mathematical results are reinterpreted in a biological context in order to gain insight into how cells, tissues, and organisms operate.

Computational Fluid Mechanics

I am particularly interested in the mechanics of fluids and complex fluids, and transport processes therein, all of which are important in biological and physiological systems. My mathematical training focuses on techniques for solving and analyzing partial differential equations (PDEs), as well as numerical methods for complex materials. I have worked on developing an Immersed Boundary (IB) method for poro-elastic materials in the context of cellular modelling, as well as integration of electro-diffusion equations into models of viscous two-phase media (in the context of gastric mucus). I have also developed models of strain relaxation in filamentous actin networks in emulsion droplets.

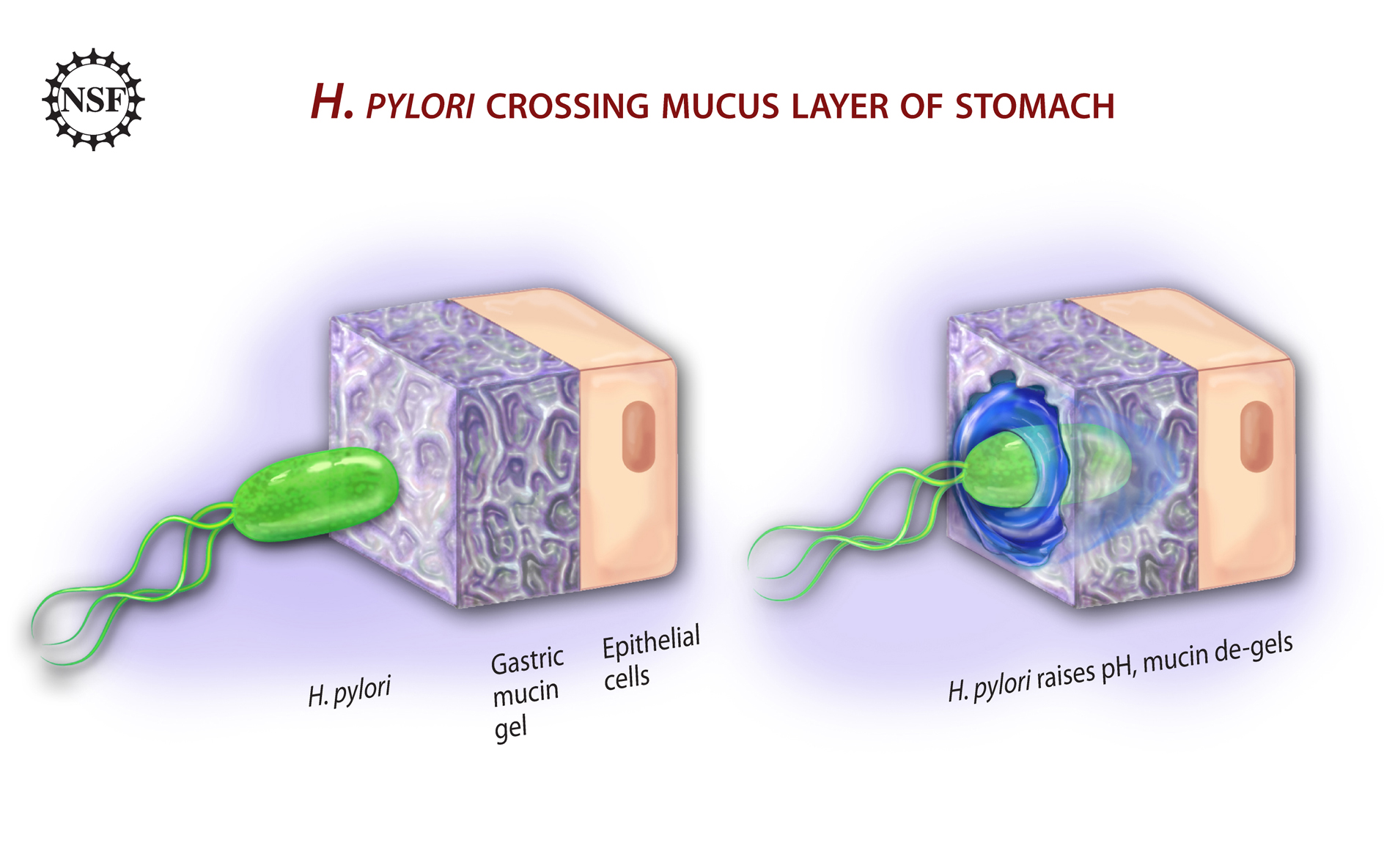
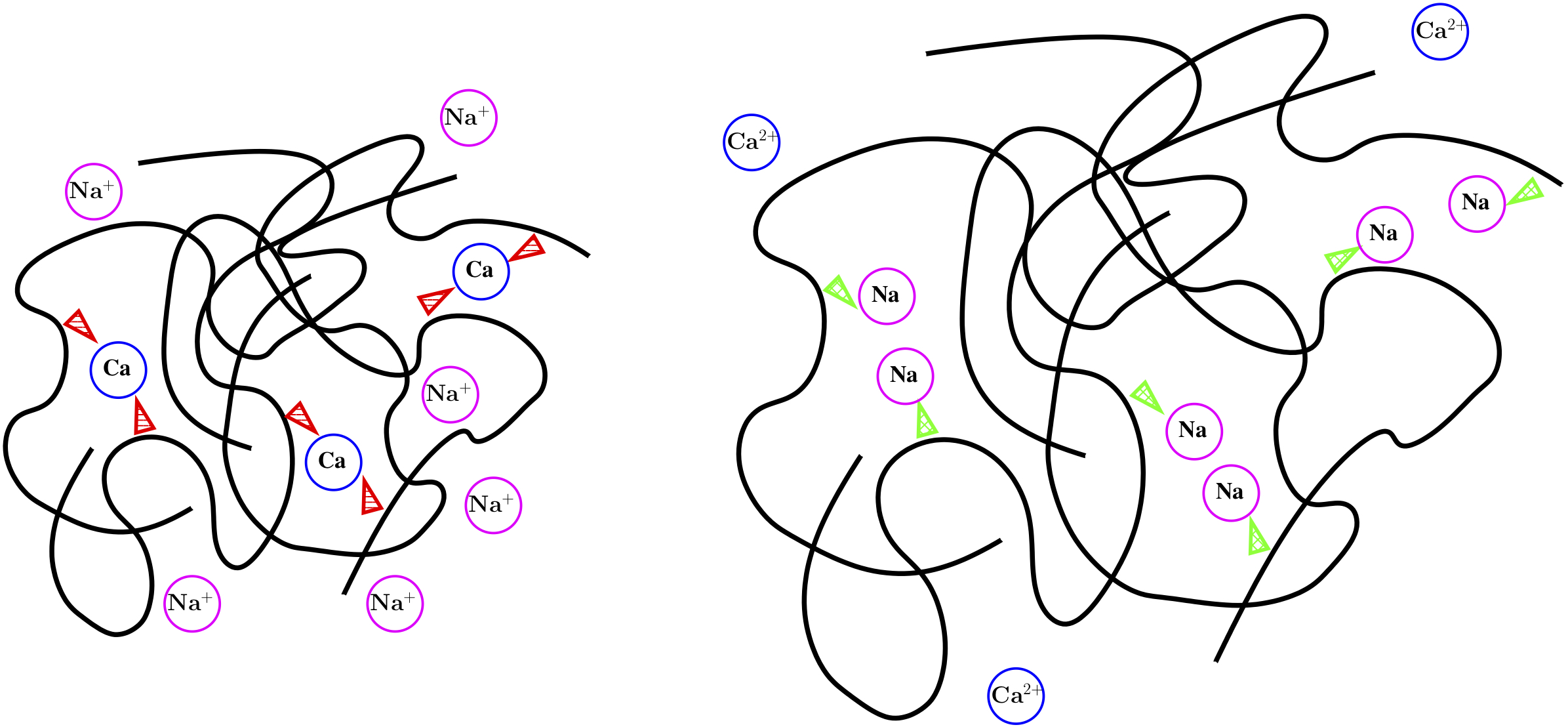
Gastric Mucus Barrier Function

I am partially supported by an NIH grant to conduct research focused on using mathematical models and experimental data to explain how the gastric mucus layer is maintained and protects the stomach wall. I am focused on how the mechanics and rheology of the mucus itself interact with the electro-chemistry of stomach acid to create a protective barrier. This barrier has the physiological task of protecting the stomach wall from acid, digestive enzymes, and infection by various pathogens. Broadly, this project involves investigation of the mechanics of hydrated polymeric gels, as well as elecro-diffusive transport within complex media.
This project is a large-scale collaboration between numerous researchers. Modelling/simulation is done in collaboration with Dr. Aaron Fogelson, Dr. James Keener, and Dr. Henry Fu (University of Utah), as well as Dr. Jian Du (Florida Institute of Technology). Experimental work is performed by the labs of Dr. James Wilking and Dr. Diane Bimczok (Montana State University), as well as Dr. Rama Bansil (Boston University).

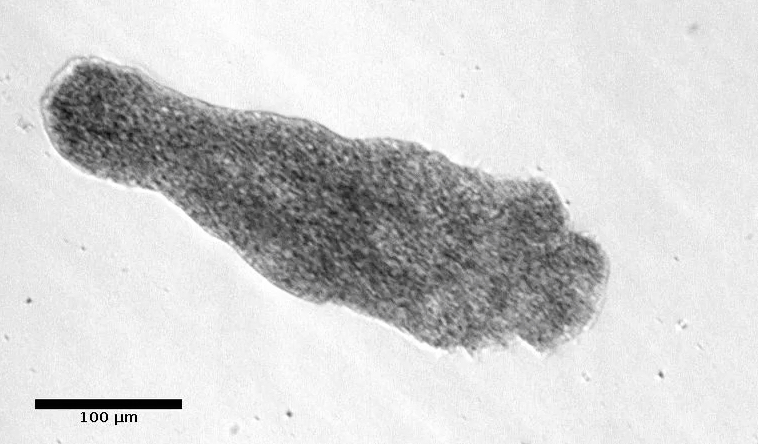
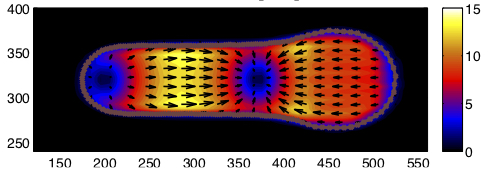
Cytoplasmic Streaming & Cell Crawling

An ongoing project started during my dissertation (with Dr. Robert Guy) focuses on analytical and numerical models of cytoplasmic streaming witnessed in the slime mold Physarum. This work is performed in conjunction with Dr. Toshi Nakagaki, as well as the lab of Dr. Juan Carlos del Álamo. Through the comparison of modeling predictions to traction stress microscopy and particle image velocimetry data, we explore the coordination of spatio-temporal waves necessary to drive cellular motility through cytoplasmic pumping. More recently, we are focused on understanding the physical instability that leads to the onset of cytoplasmic streaming as the organism reaches a critical size.